Because I'm a social psychologist who uses repeated-measures designs without complex, hierarchical structures (e.g. students are affected by their teachers who are affected by their schools who are affected by their districts, etc.), I'm referring to "simple" repeated measures. Here are some examples:
- Positive or negative affect measured at multiple time points
- Agreement with items that make up different subscales
- Subjective ratings measured for multiple stimuli (e.g. pictures of faces)
By "simple" I mean that there's no obvious reason to me that an analyst should assume that time points or stimuli are nested within participants. That is, in these cases above, responses at different time points or responses to different stimuli are not correlated with each other because they come from the same participants.
This point will become clearer later in this post when you see some pretty surprising results that fall out of models that specify nesting in this way. There are probably instances when an analyst might reasonably specify stimuli nested within participants, but, for now, I'm ignorant of those reasons.
Update: there are great reasons to assume subjects and stimuli are random and crossed, not nested (Treating Stimuli as a Random Factor in Social Psychology: A New and Comprehensive Solution to a Pervasive but Largely Ignored Problem).
Update: there are great reasons to assume subjects and stimuli are random and crossed, not nested (Treating Stimuli as a Random Factor in Social Psychology: A New and Comprehensive Solution to a Pervasive but Largely Ignored Problem).
Let's look at an example using fake data. Imagine you've designed 3 pictures meant to elicit varying degrees of disgust in participants: Low disgust, moderate disgust, and high disgust.
Because standard practices in psychology allow you to pre-test stimuli with very few participants, you gather only 10 participants to rate each picture on how disgusting they are.
Below I generate some data for 10 participants whose disgust ratings correlate r = .5 across images (i.e. on average, participants' ratings of picture 1 correlate r = .5 with their ratings of picture 2 and ratings of picture 3 ). The population mean ratings for pictures 1 through 3 are mean = 1, 4, and 7.
library(MASS) set.seed(1) fake <- mvrnorm(n = 10, mu = c(1,4,7), Sigma = matrix(data = c(1,.5,.5, .5,1,.5, .5,.5,1), nrow = 3, ncol = 3, byrow = TRUE)) # look at data boxplot(x = fake, names = c("Low Disgust","Moderate Disgust","High Disgust"), ylab = "Disgust")

I'll run tests soon, but, first, here's the simple null hypothesis:
Low disgust picture = Moderate disgust picture = High Disgust picture
The alternative is as simple:
Low disgust picture < Moderate disgust picture < High disgust picture
In my opinion, there's a correct analytic solution to these questions. Run three paired t-tests:
- Low disgust vs. moderate disgust
- Low disgust vs. high disgust
- Moderate disgust vs. high disgust
Compound symmetry and sphericity assumptions are satisfied (with df = 1, this will always be true). There's no reason to specify that picture is nested within subjects. There are no missing data.
This is boring and probably obvious, I know, but I promise you that standard analytic practices (i.e. repeated measures ANOVA) and other tutorials detailing multilevel model solutions to repeated measures seem to ignore this point.
That is, given this very simple research design, three paired t-tests give the correct answer to the hypotheses above, yet there are multiple cases I've seen where good-intentioned researchers and bloggers don't check whether their results conform with the "simpler" (but still correct) analytic procedures.
Below you'll see what I mean.
I coded the contrasts for all pairwise comparisons. Each contrast is labeled in the output. The intercept tests the mean of the difference scores against zero. You'd get the same results if you ran one-sample t-tests on these difference scores.
disgust.conts <- cbind("lowVmod" = c(-1,1,0), "lowVhigh" = c(-1,0,1), "modVhigh" = c(0,-1,1)) summary(object = lm(fake %*% disgust.conts ~ 1))
## Response lowVmod : ## ## Call: ## lm(formula = lowVmod ~ 1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.54309 -0.81027 0.04594 0.22895 2.83884 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 2.991 0.388 7.71 2.97e-05 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.227 on 9 degrees of freedom ## ## ## Response lowVhigh : ## ## Call: ## lm(formula = lowVhigh ~ 1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.7226 -0.2989 -0.2143 0.2531 1.5054 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 6.2402 0.2089 29.88 2.58e-10 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.6605 on 9 degrees of freedom ## ## ## Response modVhigh : ## ## Call: ## lm(formula = modVhigh ~ 1) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.4635 -0.2866 0.2430 0.6643 1.2629 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 3.2488 0.3382 9.606 4.99e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.07 on 9 degrees of freedom
Now here's the interesting part:
Can we get the same results using a multilevel model approach?
Some very smart (way smarter than me) textbook writers and researchers-who-blog claim that we can, but it's often the case that they don't compare their results to those from paired t-tests.
If you're a graduate student or a motivated PhD-holding researcher interested in learning how to analyze repeated measures data in R, you'll likely do one of two things:
- Copy the R code from Field et al.'s Discovering Statistics Using R (which is a fantastic textbook, to be sure)
- Google "repeated measures in R" and visit one of the top results, like Repeated Measures in R - Jason A. French.
Here's how you'd run the analysis using their procedure.
# convert to "long" form fake.long <- data.frame(id = rep(x = 1:10,times = 3), picture = rep(x = c("Low Disgust","Moderate Disgust","High Disgust"), each = nrow(fake)), disgust = c(fake[,1],fake[,2], fake[,3])) # rearrange picture factor fake.long$picture <- with(data = fake.long, factor(x = picture, levels = levels(picture)[c(2,3,1)],ordered = TRUE)) # set contrasts: low vs. moderate contrasts(fake.long$picture) <- cbind(c(-1,1,0)) library(nlme) # This could be right answer in some designs, but this can't be right given the research questions summary(object = lme(fixed = disgust ~ picture, data = fake.long, random = ~ 1 | id/picture, method = "REML"))
## Linear mixed-effects model fit by REML ## Data: fake.long ## AIC BIC logLik ## 87.13133 94.90635 -37.56566 ## ## Random effects: ## Formula: ~1 | id ## (Intercept) ## StdDev: 0.4845503 ## ## Formula: ~1 | picture %in% id ## (Intercept) Residual ## StdDev: 0.6668918 0.2636613 ## ## Fixed effects: disgust ~ picture ## Value Std.Error DF t-value p-value ## (Intercept) 3.892057 0.2015464 18 19.310969 0 ## picture1 1.495671 0.1603530 18 9.327363 0 ## picture2 3.873881 0.2267734 18 17.082604 0 ## Correlation: ## (Intr) pictr1 ## picture1 0 ## picture2 0 0 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -0.80775499 -0.16243419 0.04333559 0.23249220 0.64771218 ## ## Number of Observations: 30 ## Number of Groups: ## id picture %in% id ## 10 30
Before I say what I'm going to say about this result, I'll emphasize again that these authors are hundreds of times smarter than I am and I've benefited greatly from their statistics materials. Andy Field, specifically, is, to me, one of the best statistics teachers in the past few decades. Thousands (if not millions!) of students think statistics can be fun and intuitive because of his lectures, videos, and books.
That said.
His multilevel model solution to repeated measures in his textbook is wrong. By extension, so is Dr. French's blog post (which references Field et al.).
Neither author mentions why you should nest the within-subjects factor within subject. What's more, neither mentions the default covariance structure. Why do they choose to run the analysis this way and, most importantly, why don't the results match the paired t-test?
End rant.
Now, to get the right answer—that is, one that matches the results from the paired t-tests—you need two arguments in the lme() function and two functions in the nlme package:
correlation: Defaults to "no within-group correlations"
weights: Defaults to "homoscedastic within-group errors"
corSymm(): lets you specify a "general correlation structure."
varIdent(): from defaults to constant variance = 1
Without going into too many details (this post is long enough without them), to get the same results as those from the paired t-tests, you'll use the above arguments and functions to specify what's called an unstructured covariance matrix.
The unstructured covariance matrix makes no assumptions about patterns in covariances within-groups; each variance and covariance is estimated from the data (Ironically, I wrote this sentence referencing Field et al).
Use the correlation argument and corSymm() function to specify the unstructured covariance matrix, and use the weights argument and the varIdent() function to specify unique variances among the pictures. I do that below.
Quick note: I haven't figured out how to print all of contrasts in one model's output, so I have to specify contrasts individually.
Look for these t-values: 7.71, 29.88, and 9.606.
p-values will vary because calculating degrees of freedom in multilevel models is...tricky business.
# this solution converges with the multivariate approach summary(object = lme(fixed = disgust ~ picture, data = fake.long, random = ~ 1 | id, correlation = corSymm(form = ~ 1 | id), weights = varIdent(form = ~ 1 | picture), method = "REML"))
## Linear mixed-effects model fit by REML ## Data: fake.long ## AIC BIC logLik ## 84.37704 97.33541 -32.18852 ## ## Random effects: ## Formula: ~1 | id ## (Intercept) Residual ## StdDev: 0.3828687 1.033174 ## ## Correlation Structure: General ## Formula: ~1 | id ## Parameter estimate(s): ## Correlation: ## 1 2 ## 2 -0.131 ## 3 0.780 -0.559 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | picture ## Parameter estimates: ## Low Disgust Moderate Disgust High Disgust ## 1.0000000 0.5224815 0.6482276 ## Fixed effects: disgust ~ picture ## Value Std.Error DF t-value p-value ## (Intercept) 3.892057 0.2015465 18 19.310966 0 ## picture1 1.495671 0.1940031 18 7.709521 0 ## picture2 3.873881 0.1660666 18 23.327279 0 ## Correlation: ## (Intr) pictr1 ## picture1 -0.647 ## picture2 0.009 -0.448 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -2.4080013 -0.3965247 0.1140086 0.6179098 1.5761520 ## ## Number of Observations: 30 ## Number of Groups: 10
# low vs. high contrasts(fake.long$picture) <- cbind(c(-1,0,1)) summary(object = lme(fixed = disgust ~ picture, data = fake.long, random = ~ 1 | id, correlation = corSymm(form = ~ 1 | id), weights = varIdent(form = ~ 1 | picture), method = "REML"))$tTable[2,]
## Value Std.Error DF t-value p-value ## 3.120093e+00 1.044300e-01 1.800000e+01 2.987736e+01 8.618548e-17
# mod vs. high contrasts(fake.long$picture) <- cbind(c(0,-1,1)) summary(object = lme(fixed = disgust ~ picture, data = fake.long, random = ~ 1 | id, correlation = corSymm(form = ~ 1 | id), weights = varIdent(form = ~ 1 | picture), method = "REML"))$tTable[2,]
## Value Std.Error DF t-value p-value ## 1.624422e+00 1.691051e-01 1.800000e+01 9.605991e+00 1.651889e-08
Finally, below I run the repeated measures ANOVA approach, the one that makes all of the terrible assumptions that Field et al. harps on. The result is an omnibus test (i.e. more than 1 degree of freedom test), which tests the uninteresting hypothesis that some significant difference exists somewhere among the groups. This test makes the impractical assumption that the variance of the difference between any two levels of a within-subjects factor is equal across all possible pairs of levels.
This is great place to reflect on the beauty of paired t-tests (or df = 1 tests):
they automatically satisfy this assumption because a covariance matrix of two terms (i.e. a 2 x 2 matrix) must have equal variances.
Anyway, here's the omnibus test that's standard in many literatures that employ repeated measures designs, like psychology.
# the repeated measures ANOVA solution which makes all of the assumptions (i.e. compound symmetry, sphericity) everyone harps about # also--who cares about df > 1 tests? library(ez) ezANOVA(data = fake.long, dv = .(disgust), wid = .(id), within = .(picture), type = 3, detailed = TRUE)
## Warning: Converting "id" to factor for ANOVA.
## $ANOVA ## Effect DFn DFd SSn SSd F p p<.05 ## 1 (Intercept) 1 9 454.4432 10.967660 372.9135 1.236682e-08 * ## 2 picture 2 18 194.8102 9.256716 189.4075 8.131287e-13 * ## ges ## 1 0.9573925 ## 2 0.9059483 ## ## $`Mauchly's Test for Sphericity` ## Effect W p p<.05 ## 2 picture 0.6271638 0.154712 ## ## $`Sphericity Corrections` ## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05 ## 2 picture 0.728419 7.435238e-10 * 0.8330976 5.348671e-11 *
Next, I'll go through examples from Field et al.'s texbook and from a few blogs I've stumbled on.
In doing so, I'm not trying to burn anyone.
Rather, I'm trying to demonstrate how you'd translate the "paired t-test method" (a.k.a. the multivariate approach) to the multilevel model approach.
This should come in handy when you have missing data, or many, many repeated measures, or both because, in these cases, paired t-tests break down:
- They make you exclude incomplete cases which contain otherwise valuable information.
- They require you to structure your data in impractical ways (e.g. imagine 50 or 100 or 400 trials measuring reaction time!).
You need multilevel models to get the "right" answer in these scenarios.
Discovering Statistics Using R Chapter 14 example
Load data
# url to data LooksOrPersonality.url <- "http://www.statisticshell.com/r_files/LooksOrPersonality.dat" # read data LooksOrPersonality <- read.delim(file = LooksOrPersonality.url, header = TRUE) # look at data boxplot(x = LooksOrPersonality[,-1:-2], ylab = "Date Rating")

Test contrasts: multivariate approach
# set contrasts in a list LooksOrPersonality.conts <- list(AttractivevsUgly = c(1,1,-2,1,1,-2,1,1,-2), AttractvsAv = c(1,-1,0,1,-1,0,1,-1,0), SomevsNone = c(1,1,1,1,1,1,-2,-2,-2), HivsAv = c(1,1,1,-1,-1,-1,0,0,0)) # gender contrast contrasts(LooksOrPersonality$gender) <- contr.sum(2) # loop through each with sapply sapply(X = LooksOrPersonality.conts, FUN = function(x){ summary(object = lm(cbind(att_high,av_high,ug_high,att_some,av_some,ug_some,att_none,av_none,ug_none) %*% x ~ 1, data = LooksOrPersonality)) }, simplify = FALSE, USE.NAMES = TRUE)
## $AttractivevsUgly ## ## Call: ## lm(formula = cbind(att_high, av_high, ug_high, att_some, av_some, ## ug_some, att_none, av_none, ug_none) %*% x ~ 1, data = LooksOrPersonality) ## ## Residuals: ## Min 1Q Median 3Q Max ## -76.75 -56.00 -0.75 52.25 78.25 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 114.75 12.25 9.368 1.49e-08 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 54.78 on 19 degrees of freedom ## ## ## $AttractvsAv ## ## Call: ## lm(formula = cbind(att_high, av_high, ug_high, att_some, av_some, ## ug_some, att_none, av_none, ug_none) %*% x ~ 1, data = LooksOrPersonality) ## ## Residuals: ## Min 1Q Median 3Q Max ## -39.95 -15.70 5.05 14.05 34.05 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.950 5.119 8.391 8.2e-08 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 22.89 on 19 degrees of freedom ## ## ## $SomevsNone ## ## Call: ## lm(formula = cbind(att_high, av_high, ug_high, att_some, av_some, ## ug_some, att_none, av_none, ug_none) %*% x ~ 1, data = LooksOrPersonality) ## ## Residuals: ## Min 1Q Median 3Q Max ## -83.40 -53.15 2.10 55.10 85.60 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 128.40 13.19 9.734 8.11e-09 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 58.99 on 19 degrees of freedom ## ## ## $HivsAv ## ## Call: ## lm(formula = cbind(att_high, av_high, ug_high, att_some, av_some, ## ug_some, att_none, av_none, ug_none) %*% x ~ 1, data = LooksOrPersonality) ## ## Residuals: ## Min 1Q Median 3Q Max ## -41.4 -18.4 -2.9 19.1 54.6 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 38.400 5.649 6.798 1.72e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 25.26 on 19 degrees of freedom
Test contrasts: multilevel model approach
Look for these t-values: 9.368, 8.391, and 9.734
# reformat as "long" data LooksOrPersonality.long <- with(data = LooksOrPersonality, data.frame(participant = rep(x = participant, times = 9), personality = rep(x = c("Charismatic","Average","Dullard"), each = 60), looks = rep(x = c("Attractive","Average","Ugly"), each = nrow(LooksOrPersonality), times = 3), gender = rep(x = gender, times = 9), rating = c(att_high, av_high, ug_high, att_some, av_some, ug_some, att_none, av_none, ug_none))) # factor levels need to be re-ordered (only for personality) LooksOrPersonality.long$personality <- with(data = LooksOrPersonality.long, factor(x = personality, levels = levels(personality)[c(2,1,3)], labels = levels(personality)[c(2,1,3)])) # contrasts contrasts(LooksOrPersonality.long$personality) <- cbind("SomevsNone" = c(1, 1, -2), "HivsAv" = c(1, -1, 0)) contrasts(LooksOrPersonality.long$looks) <- cbind("AttractivevsUgly" = c(1, 1, -2), "AttractvsAv" = c(1, -1, 0)) contrasts(LooksOrPersonality.long$gender) <- contr.sum(2) summary(object = lme(fixed = rating ~ looks*personality, data = LooksOrPersonality.long, random = ~ 1 | participant, correlation = corSymm(form = ~ 1 | participant), weights = varIdent(form = ~ 1 | looks*personality), method = "REML", control = lmeControl(msMaxIter = 1000)))
## Linear mixed-effects model fit by REML ## Data: LooksOrPersonality.long ## AIC BIC logLik ## 1241.062 1413.853 -565.531 ## ## Random effects: ## Formula: ~1 | participant ## (Intercept) Residual ## StdDev: 0.5126321 6.03483 ## ## Correlation Structure: General ## Formula: ~1 | participant ## Parameter estimate(s): ## Correlation: ## 1 2 3 4 5 6 7 8 ## 2 0.207 ## 3 0.210 0.390 ## 4 -0.121 -0.282 -0.218 ## 5 0.385 -0.106 -0.232 -0.299 ## 6 0.193 0.256 0.276 0.221 -0.026 ## 7 -0.152 -0.271 -0.901 0.095 0.230 -0.352 ## 8 0.141 0.156 -0.114 0.030 0.137 -0.138 0.162 ## 9 0.182 -0.103 0.081 0.034 0.190 -0.109 -0.032 -0.041 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | looks * personality ## Parameter estimates: ## Attractive*Charismatic Average*Charismatic Ugly*Charismatic ## 1.0000000 1.3266234 2.6952147 ## Attractive*Average Average*Average Ugly*Average ## 1.0187832 0.8764644 0.9034228 ## Attractive*Dullard Average*Dullard Ugly*Dullard ## 3.1046466 0.6381693 0.5321547 ## Fixed effects: rating ~ looks * personality ## Value Std.Error DF ## (Intercept) 68.56667 0.4715430 152 ## looksAttractivevsUgly 6.37500 0.6804716 152 ## looksAttractvsAv 7.15833 0.8531238 152 ## personalitySomevsNone 7.13333 0.7328202 152 ## personalityHivsAv 6.40000 0.9414292 152 ## looksAttractivevsUgly:personalitySomevsNone 1.10000 0.1455628 152 ## looksAttractvsAv:personalitySomevsNone -1.95833 0.7120553 152 ## looksAttractivevsUgly:personalityHivsAv -2.30000 0.5136021 152 ## looksAttractvsAv:personalityHivsAv -3.52500 0.7510762 152 ## t-value p-value ## (Intercept) 145.40914 0.0000 ## looksAttractivevsUgly 9.36850 0.0000 ## looksAttractvsAv 8.39073 0.0000 ## personalitySomevsNone 9.73408 0.0000 ## personalityHivsAv 6.79817 0.0000 ## looksAttractivevsUgly:personalitySomevsNone 7.55687 0.0000 ## looksAttractvsAv:personalitySomevsNone -2.75025 0.0067 ## looksAttractivevsUgly:personalityHivsAv -4.47817 0.0000 ## looksAttractvsAv:personalityHivsAv -4.69327 0.0000 ## Correlation: ## (Intr) lksAtU lksAtA prsnSN ## looksAttractivevsUgly 0.056 ## looksAttractvsAv -0.084 0.753 ## personalitySomevsNone 0.119 -0.910 -0.797 ## personalityHivsAv 0.233 -0.704 -0.788 0.733 ## looksAttractivevsUgly:personalitySomevsNone -0.028 -0.160 -0.139 0.236 ## looksAttractvsAv:personalitySomevsNone -0.044 -0.845 -0.628 0.862 ## looksAttractivevsUgly:personalityHivsAv 0.194 0.784 0.561 -0.646 ## looksAttractvsAv:personalityHivsAv 0.071 0.157 0.098 -0.146 ## prsnHA lAU:SN lAA:SN lAU:HA ## looksAttractivevsUgly ## looksAttractvsAv ## personalitySomevsNone ## personalityHivsAv ## looksAttractivevsUgly:personalitySomevsNone 0.058 ## looksAttractvsAv:personalitySomevsNone 0.555 0.294 ## looksAttractivevsUgly:personalityHivsAv -0.582 -0.163 -0.726 ## looksAttractvsAv:personalityHivsAv -0.098 0.193 -0.144 0.035 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -2.39718838 -0.77327710 0.01327948 0.69058961 2.17611793 ## ## Number of Observations: 180 ## Number of Groups: 20
Sometimes combining factors into one factor can make writing contrasts a little easier, especially when translating contrasts from the multivariate approach.
Again, look for these t-values: 9.368, 8.391, and 9.734
# using a grouping variable LooksOrPersonality.long$combo <- with(data = LooksOrPersonality.long, interaction(looks, personality)) # same contrasts above applied over the grouping variable contrasts(LooksOrPersonality.long$combo) <- cbind(c(1,1,-2,1,1,-2,1,1,-2), c(1,-1,0,1,-1,0,1,-1,0), c(1,1,1,1,1,1,-2,-2,-2), c(1,1,1,-1,-1,-1,0,0,0)) # fit model and summarise summary(object = lme(fixed = rating ~ combo, data = LooksOrPersonality.long, random = ~ 1 | participant, correlation = corSymm(form = ~ 1 | participant), weights = varIdent(form = ~ 1 | combo), method = "REML", control = lmeControl(msMaxIter = 1000)))
## Linear mixed-effects model fit by REML ## Data: LooksOrPersonality.long ## AIC BIC logLik ## 1231.122 1403.914 -560.5612 ## ## Random effects: ## Formula: ~1 | participant ## (Intercept) Residual ## StdDev: 0.5126313 6.034828 ## ## Correlation Structure: General ## Formula: ~1 | participant ## Parameter estimate(s): ## Correlation: ## 1 2 3 4 5 6 7 8 ## 2 0.207 ## 3 0.210 0.390 ## 4 -0.121 -0.282 -0.218 ## 5 0.385 -0.106 -0.232 -0.299 ## 6 0.193 0.256 0.276 0.221 -0.026 ## 7 -0.152 -0.271 -0.901 0.095 0.230 -0.352 ## 8 0.141 0.156 -0.114 0.030 0.137 -0.138 0.162 ## 9 0.182 -0.103 0.081 0.034 0.190 -0.109 -0.032 -0.041 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | combo ## Parameter estimates: ## Attractive.Charismatic Average.Charismatic Ugly.Charismatic ## 1.0000000 1.3266256 2.6952335 ## Attractive.Average Average.Average Ugly.Average ## 1.0187840 0.8764651 0.9034222 ## Attractive.Dullard Average.Dullard Ugly.Dullard ## 3.1046550 0.6381676 0.5321533 ## Fixed effects: rating ~ combo ## Value Std.Error DF t-value p-value ## (Intercept) 68.56667 0.4715376 152 145.41081 0.0000 ## combo1 6.37500 0.6804763 152 9.36844 0.0000 ## combo2 7.15833 0.8531288 152 8.39068 0.0000 ## combo3 7.13333 0.7328223 152 9.73406 0.0000 ## combo4 6.40000 0.9414326 152 6.79815 0.0000 ## combo5 -5.33617 1.9626663 152 -2.71884 0.0073 ## combo6 7.46880 1.3188934 152 5.66293 0.0000 ## combo7 -3.51611 2.3558054 152 -1.49253 0.1376 ## combo8 10.30255 1.0619099 152 9.70191 0.0000 ## Correlation: ## (Intr) combo1 combo2 combo3 combo4 combo5 combo6 combo7 ## combo1 0.056 ## combo2 -0.084 0.753 ## combo3 0.119 -0.910 -0.797 ## combo4 0.233 -0.704 -0.788 0.733 ## combo5 0.145 0.755 0.552 -0.662 -0.544 ## combo6 -0.104 0.358 0.297 -0.493 -0.181 0.462 ## combo7 -0.076 -0.838 -0.613 0.823 0.563 -0.645 -0.324 ## combo8 -0.092 -0.195 -0.137 0.218 0.099 0.044 0.133 0.394 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -2.39719501 -0.77327670 0.01328116 0.69059119 2.17612583 ## ## Number of Observations: 180 ## Number of Groups: 20
Occam's Pocket Knife Blog
Translating SPSS to R: Factorial Repeated Measures
library(xlsx)
# path to data (found on blog too) elashoff.path <- "~/Desktop/analysis-examples/Multivariate and Multilevel Model Approaches to Repeated Measures in R and SPSS/elashoff.xls" # read data elashoff <- read.xlsx(file = elashoff.path, sheetIndex = 1, as.data.frame = TRUE, header = TRUE) # look at data boxplot(x = elashoff[,-1:-2], ylab = "Alertness")

Test contrasts: multivariate approach
# test one contrast summary(object = lm(cbind(T1D1,T1D2,T1D3,T2D1,T2D2,T2D3,T3D1,T3D2,T3D3) %*% c(1,0,-1,-2,0,2,1,0,-1) ~ 1, data = elashoff))
## ## Call: ## lm(formula = cbind(T1D1, T1D2, T1D3, T2D1, T2D2, T2D3, T3D1, ## T3D2, T3D3) %*% c(1, 0, -1, -2, 0, 2, 1, 0, -1) ~ 1, data = elashoff) ## ## Residuals: ## Min 1Q Median 3Q Max ## -23.312 -5.312 2.188 6.688 21.688 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 2.312 3.018 0.766 0.455 ## ## Residual standard error: 12.07 on 15 degrees of freedom
Test contrasts: multilevel model approach
Look for this t-value: 0.766
elashoff.long <- with(data = elashoff, data.frame(Snum = rep(x = Snum, times = 9), Group = rep(x = Group, times = 9), type = rep(x = paste0("Type",1:3), each = 48), dose = rep(x = paste0("Dose",1:3), each = nrow(elashoff), times = 3), alertness = c(T1D1,T1D2,T1D3,T2D1,T2D2,T2D3,T3D1,T3D2,T3D3))) # contrasts elashoff.long$Group <- with(data = elashoff.long, factor(Group)) contrasts(elashoff.long$Group) <- contr.sum(2) contrasts(elashoff.long$type) <- cbind(c(1,-2,1)) contrasts(elashoff.long$dose) <- contr.poly(3) # fit model and summarise summary(object = lme(fixed = alertness ~ type*dose, data = elashoff.long, random = ~ 1 | Snum, correlation = corSymm(form = ~ 1 | Snum), weights = varIdent(form = ~ 1 | type*dose), method = "REML", control = lmeControl(msMaxIter = 1000)))
## Linear mixed-effects model fit by REML ## Data: elashoff.long ## AIC BIC logLik ## 816.649 976.4392 -353.3245 ## ## Random effects: ## Formula: ~1 | Snum ## (Intercept) Residual ## StdDev: 0.979239 3.342202 ## ## Correlation Structure: General ## Formula: ~1 | Snum ## Parameter estimate(s): ## Correlation: ## 1 2 3 4 5 6 7 8 ## 2 0.781 ## 3 -0.630 -0.411 ## 4 0.299 0.106 -0.558 ## 5 0.102 0.035 -0.136 0.721 ## 6 0.192 0.201 -0.212 0.773 0.632 ## 7 0.680 0.467 -0.726 0.351 -0.155 0.254 ## 8 0.681 0.803 -0.293 0.035 -0.039 0.085 0.348 ## 9 -0.070 0.008 0.613 -0.328 0.121 -0.066 -0.516 0.044 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | type * dose ## Parameter estimates: ## Type1*Dose1 Type1*Dose2 Type1*Dose3 Type2*Dose1 Type2*Dose2 Type2*Dose3 ## 1.0000000 0.7310784 0.8519590 1.7828051 1.8291714 1.7995607 ## Type3*Dose1 Type3*Dose2 Type3*Dose3 ## 1.3455650 1.3370819 1.3659252 ## Fixed effects: alertness ~ type * dose ## Value Std.Error DF t-value p-value ## (Intercept) 23.555556 0.6149712 120 38.30351 0.0000 ## type1 -1.211806 0.4716275 120 -2.56941 0.0114 ## type2 0.250434 0.2595108 120 0.96502 0.3365 ## dose.L 4.272103 0.8374583 120 5.10127 0.0000 ## dose.Q 0.221134 0.4523375 120 0.48887 0.6258 ## type1:dose.L -0.272531 0.3556255 120 -0.76634 0.4450 ## type2:dose.L -1.281250 0.7541113 120 -1.69902 0.0919 ## type1:dose.Q -0.335954 0.3769222 120 -0.89131 0.3745 ## type2:dose.Q 0.306717 0.4905138 120 0.62530 0.5330 ## Correlation: ## (Intr) type1 type2 dose.L dose.Q ty1:.L ty2:.L ty1:.Q ## type1 -0.536 ## type2 0.417 0.165 ## dose.L -0.252 0.141 -0.283 ## dose.Q -0.218 -0.073 -0.070 0.079 ## type1:dose.L -0.394 0.050 -0.376 0.586 -0.084 ## type2:dose.L 0.300 0.079 0.212 0.381 -0.401 0.379 ## type1:dose.Q -0.230 -0.075 -0.411 0.519 -0.067 0.731 0.394 ## type2:dose.Q -0.063 -0.222 -0.167 -0.004 0.634 -0.039 -0.126 0.257 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -2.46340295 -0.61760472 0.02451049 0.73473991 2.52945059 ## ## Number of Observations: 144 ## Number of Groups: 16
Using a grouping variable (i.e. combing dose and type)
Again, look for this t-value: 0.766
# create combo of type and dose elashoff.long$type.dose <- with(data = elashoff.long, interaction(dose,type)) contrasts(elashoff.long$type.dose) <- cbind(c(c(1, 0, -1) %o% c(1, -2, 1))) # fit model and summarise summary(object = lme(fixed = alertness ~ type.dose, data = elashoff.long, random = ~ 1 | Snum, correlation = corSymm(form = ~ 1 | Snum), weights = varIdent(form = ~ 1 | type.dose), method = "REML", control = lmeControl(msMaxIter = 1000)))
## Linear mixed-effects model fit by REML ## Data: elashoff.long ## AIC BIC logLik ## 809.3642 969.1543 -349.6821 ## ## Random effects: ## Formula: ~1 | Snum ## (Intercept) Residual ## StdDev: 0.9792645 3.342183 ## ## Correlation Structure: General ## Formula: ~1 | Snum ## Parameter estimate(s): ## Correlation: ## 1 2 3 4 5 6 7 8 ## 2 0.781 ## 3 -0.630 -0.411 ## 4 0.299 0.106 -0.558 ## 5 0.102 0.035 -0.136 0.721 ## 6 0.192 0.201 -0.212 0.773 0.632 ## 7 0.680 0.467 -0.726 0.351 -0.155 0.254 ## 8 0.681 0.803 -0.293 0.035 -0.039 0.085 0.348 ## 9 -0.070 0.008 0.613 -0.328 0.121 -0.066 -0.516 0.044 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | type.dose ## Parameter estimates: ## Dose1.Type1 Dose2.Type1 Dose3.Type1 Dose1.Type2 Dose2.Type2 Dose3.Type2 ## 1.0000000 0.7310813 0.8519575 1.7828108 1.8291802 1.7995798 ## Dose1.Type3 Dose2.Type3 Dose3.Type3 ## 1.3455713 1.3370953 1.3659308 ## Fixed effects: alertness ~ type.dose ## Value Std.Error DF t-value p-value ## (Intercept) 23.555556 0.6149724 120 38.30344 0.0000 ## type.dose1 0.192708 0.2514682 120 0.76633 0.4450 ## type.dose2 3.373557 0.9247224 120 3.64818 0.0004 ## type.dose3 0.955736 1.5135378 120 0.63146 0.5289 ## type.dose4 2.978878 1.3080898 120 2.27727 0.0245 ## type.dose5 7.189520 1.0307908 120 6.97476 0.0000 ## type.dose6 -2.040801 0.8710002 120 -2.34305 0.0208 ## type.dose7 0.166378 0.8853183 120 0.18793 0.8512 ## type.dose8 2.623557 1.0599055 120 2.47527 0.0147 ## Correlation: ## (Intr) typ.d1 typ.d2 typ.d3 typ.d4 typ.d5 typ.d6 typ.d7 ## type.dose1 0.394 ## type.dose2 -0.616 -0.474 ## type.dose3 0.539 0.374 -0.520 ## type.dose4 0.374 -0.339 -0.116 0.486 ## type.dose5 0.333 -0.009 0.168 0.553 0.587 ## type.dose6 -0.257 0.532 -0.164 0.092 -0.626 -0.462 ## type.dose7 0.043 0.247 -0.185 -0.412 -0.528 -0.467 0.099 ## type.dose8 -0.197 -0.543 0.595 -0.607 -0.022 0.052 -0.482 -0.118 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -2.46340782 -0.61761337 0.02451318 0.73473868 2.52943642 ## ## Number of Observations: 144 ## Number of Groups: 16
Jason French's (Northwestern) example
Repeated Measures in R
# path to data from the personality project appendix3.url <- "http://personality-project.org/r/datasets/R.appendix3.data" # read data appendix3 <- read.table(file = appendix3.url, header = TRUE) # look at data with(data = appendix3, boxplot(Recall ~ Valence, ylab = "Recall"))

Test contrasts: multivariate approach
# reformat data to "wide" form appendix3.wide <- reshape(data = appendix3, timevar = "Valence", idvar = "Subject", direction = "wide", drop = "Observation") # contrasts appendix3.conts <- cbind("neutVneg" = c(-1,1,0), "neutVpos" = c(0,-1,1), "negVpos" = c(-1,0,1)) # test contrasts summary(lm(cbind(Recall.Neg,Recall.Neu,Recall.Pos) %*% appendix3.conts ~ 1, data = appendix3.wide))
## Response neutVneg : ## ## Call: ## lm(formula = neutVneg ~ 1, data = appendix3.wide) ## ## Residuals: ## 1 4 7 10 13 ## -0.8 -0.8 2.2 4.2 -4.8 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -16.20 1.53 -10.59 0.00045 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 3.421 on 4 degrees of freedom ## ## ## Response neutVpos : ## ## Call: ## lm(formula = neutVpos ~ 1, data = appendix3.wide) ## ## Residuals: ## 1 4 7 10 13 ## 1.6 -1.4 1.6 -0.4 -1.4 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 28.4000 0.6782 41.87 1.94e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.517 on 4 degrees of freedom ## ## ## Response negVpos : ## ## Call: ## lm(formula = negVpos ~ 1, data = appendix3.wide) ## ## Residuals: ## 1 4 7 10 13 ## 0.8 -2.2 3.8 3.8 -6.2 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 12.200 1.908 6.395 0.00307 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 4.266 on 4 degrees of freedom
Test contrasts: multilevel model approach
Look for these t-values: -10.59, 41.87, and 6.395
# neutral vs. positive contrast contrasts(appendix3$Valence) <- cbind("neutVpos" = c(0,-1,1)) # fit model and summarise summary(object = lme(fixed = Recall ~ Valence, data = appendix3, random = ~ 1 | Subject, correlation = corSymm(form = ~ 1 | Subject), weights = varIdent(form = ~ 1 | Valence), method = "REML"))
## Linear mixed-effects model fit by REML ## Data: appendix3 ## AIC BIC logLik ## 79.30066 84.14973 -29.65033 ## ## Random effects: ## Formula: ~1 | Subject ## (Intercept) Residual ## StdDev: 2.141192 3.258112 ## ## Correlation Structure: General ## Formula: ~1 | Subject ## Parameter estimate(s): ## Correlation: ## 1 2 ## 2 0.152 ## 3 0.114 0.995 ## Variance function: ## Structure: Different standard deviations per stratum ## Formula: ~1 | Valence ## Parameter estimates: ## Neg Neu Pos ## 1.0000000 0.5057577 0.9664663 ## Fixed effects: Recall ~ Valence ## Value Std.Error DF t-value p-value ## (Intercept) 26.466667 1.3232954 8 20.00057 0.0000 ## ValenceneutVpos 14.200000 0.3391164 8 41.87353 0.0000 ## Valence -1.632993 1.3844375 8 -1.17954 0.2721 ## Correlation: ## (Intr) VlncnV ## ValenceneutVpos 0.561 ## Valence -0.004 0.565 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -1.4743931 -0.8690824 -0.1993220 1.0182116 1.1012722 ## ## Number of Observations: 15 ## Number of Groups: 5
# neutral vs. negative contrast contrasts(appendix3$Valence) <- cbind("neutVneg" = c(-1,1,0)) summary(object = lme(fixed = Recall ~ Valence, data = appendix3, random = ~ 1 | Subject, correlation = corSymm(form = ~ 1 | Subject), weights = varIdent(form = ~ 1 | Valence), method = "REML", control = lmeControl(msMaxIter = 1000)))$tTable[2,]
## Value Std.Error DF t-value p-value ## -8.100000e+00 7.648531e-01 8.000000e+00 -1.059027e+01 5.523001e-06
# negative vs. positive contrast contrasts(appendix3$Valence) <- cbind("negVpos" = c(-1,0,1)) summary(object = lme(fixed = Recall ~ Valence, data = appendix3, random = ~ 1 | Subject, correlation = corSymm(form = ~ 1 | Subject), weights = varIdent(form = ~ 1 | Valence), method = "REML", control = lmeControl(msMaxIter = 1000)))$tTable[2,]
## Value Std.Error DF t-value p-value ## 6.1000000000 0.9539392658 8.0000000000 6.3945370721 0.0002103541
I almost forgot about SPSS.
To run repeated measures in SPSS the "right" way (i.e. single df tests that test interesting research questions and automatically satisfy sphericity), I use the GLM command.
First, I write all of these data as csv files and output SPSS syntax that will read them and label their factors. All of these datasets and syntax files (.sps) are available at my bitbucket repository.
# set working directory setwd(dir = "~/Desktop/analysis-examples/Multivariate and Multilevel Model Approaches to Repeated Measures in R and SPSS/") # the hypothetical pretest data I made fake.wide <- data.frame(id = 1:10,fake) names(fake.wide) <- c("id","low","moderate","high") foreign:::writeForeignSPSS(df = fake.wide, datafile = "fake.wide.csv", codefile = "fake.wide.sps", varnames = names(fake.wide)) # bushtucker foreign:::writeForeignSPSS(df = bushtucker, datafile = "bushtucker.csv", codefile = "bushtucker.sps", varnames = names(bushtucker)) # LooksOrPersonality foreign:::writeForeignSPSS(df = LooksOrPersonality, datafile = "LooksOrPersonality.csv", codefile = "LooksOrPersonality.sps", varnames = names(LooksOrPersonality)) # elashoff foreign:::writeForeignSPSS(df = elashoff, datafile = "elashoff.csv", codefile = "elashoff.sps", varnames = names(elashoff)) # appendix3.wide foreign:::writeForeignSPSS(df = appendix3.wide, datafile = "appendix3.wide.csv", codefile = "appendix3.wide.sps", varnames = names(appendix3.wide))
Next I run one example in SPSS because otherwise I'd be printing gobs of unnecessary output.
This is the pre-test example from the beginning of this post.
Testing contrasts: multivariate approach
data list file= "C:\Users\nickmm\Desktop\nmmichalak-analysis-examples-939823e544d9\Multivariate and "+ "Multilevel Model Approaches to Repeated Measures in R and SPSS\fake.wide.csv" free (",")
/id low moderate high.
variable labels
id "id"
low "low"
moderate "moderate"
high "high".
execute.
glm low moderate high
/wsfactor picture 3 simple
/wsdesign picture.
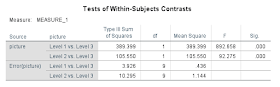
Take the square root of the F values and you'll get the same t-values as in the R example:
√892.658 = 29.88
√92.275 = 9.61
Testing contrasts: the multilevel model approach
data list file= "C:\Users\nickmm\Desktop\nmmichalak-analysis-examples-43db191e5897\Multivariate and "+
"Multilevel Model Approaches to Repeated Measures in R and SPSS\fake.long.csv" free (",")
/ id picture disgust .
variable labels
id "id"
picture "picture"
disgust "disgust".
value labels
/picture
1 "Low Disgust"
2 "Moderate Disgust"
3 "High Disgust".
execute.
mixed disgust by picture
/fixed = picture
/repeated = picture | subject(id) covtype(un)
/test = 'lowVmod' picture -1 1 0
/test = 'lowVhigh' picture -1 0 1
/test = 'modVhigh' picture 0 -1 1.
I hope this has been useful.
Happy R,
Nick



No comments:
Post a Comment